 | Chapter 4: Graphics with AWT and Java 2D |  |

One of the most fundamental abstractions in Java 2D is the java.awt.Shape. This interface describes a shape, obviously. But note that the Java 2D definition of a shape does not require the shape to enclose an area--a Shape object may represent an open curve such as a line or parabola just as easily as it represents a closed curve such as a rectangle or circle. If an open curve is passed to a graphics operation (such as fill()) that requires a closed curve, the curve is implicitly closed by adding a straight-line segment between its end points. A Java 2D shape is sometimes referred to as a "path," because it describes the path a pen would follow to draw the shape.
The Java 2D Graphics2D class defines some very fundamental operations on Shape objects: draw() draws a Shape; fill() fills a Shape; clip() restricts the current drawing region to the specified Shape; hit() tests whether a given rectangle falls in or on a given shape. In addition, the AffineTransform class has methods that allow Shape objects to be arbitrarily scaled, rotated, translated, and sheared. Because the Shape interface is used throughout Java 2D, these fundamental operations on shapes are quite powerful. For example, the individual glyphs of a font can be represented as Shape objects, meaning they can be individually scaled, rotated, drawn, filled, and so on.
Java 2D contains a number of predefined Shape implementations, many of which are part of the java.awt.geom package. Note that some basic geometric shapes have multiple Shape implementations, where each implementation uses a different data type to store coordinates. Table 4-7 lists these predefined Shape implementations.
To draw a circle inside a square, for example, you can use code like this:
Graphics2D g; // Initialized elsewhere Shape square = new Rectangle2D.Float(100.0f, 100.0f, 100.0f, 100.0f); Shape circle = new Ellipse2D.Float(100.0f, 100.0f, 100.0f, 100.0f); g.draw(square); g.draw(circle);
In addition to these basic predefined shapes, the java.awt.geom package also contains two powerful classes for defining complex shapes. The Area class allows you to define a shape that is the union or intersection of other shapes. It also allows you to subtract one shape from another or define a shape that is the exclusive OR of two shapes. For example, the following code allows you to fill the shape that results from subtracting a circle from a square:
Graphics2D g; // Initialized elsewhere Shape square = new Rectangle2D.Float(100.0f, 100.0f, 100.0f, 100.0f); Shape circle = new Ellipse2D.Float(100.0f, 100.0f, 100.0f, 100.0f); Area difference = new Area(square); difference.subtract(circle); g.fill(difference);
The GeneralPath class allows you to describe a Shape as a sequence of line segments and Bezier curve segments. You create such a general shape by calling the moveTo(), lineTo(), quadTo(), and curveTo() methods of GeneralPath. GeneralPath also allows you to append entire Shape objects to the path you are defining.
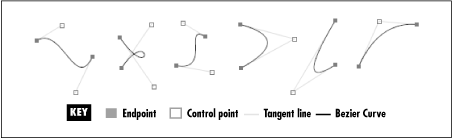
A Bezier curve is a smooth curve between two end points, with a shape described by one or more control points. Java 2D makes extensive low-level use of quadratic and cubic Bezier curves. A quadratic Bezier curve uses one control point, while a cubic Bezier curve uses two control points. There is some moderately complex mathematics behind Bezier curves, but for most Java 2D programmers, an intuitive understanding of these curves is sufficient. Figure 4-1 shows three quadratic and three cubic Bezier curves and illustrates how the position of the control points affects the shape of the curve.
Java 2D can perform some very general operations on arbitrary Shape objects. In order to make this possible, the Shape interface exposes a quite general description of the desired shape. For example, the getBounds() and getBounds2D() methods return a bounding box for the shape. The various contains() methods test whether a given point or rectangle is enclosed by the shape. The intersects() methods test whether a given rectangle touches or overlaps the shape. These methods enable clipping, hit detection, and similar operations.
The getBounds(), contains(), and intersects() methods are important, but they do not say anything about how to draw the shape. This is the job of getPathIterator(), which returns a java.awt.geom.PathIterator object that breaks a Shape down into a sequence of individual line and curve segments that Java 2D can handle at a primitive level. The PathIterator interface is basically the opposite of GeneralPath. While GeneralPath allows a Shape to be built of line and curve segments, PathIterator breaks a Shape down into its component line and curve segments.
Shape defines two getPathIterator() methods. The two-argument version of this method returns a PathIterator that describes the shape in terms of line segments only (i.e., it cannot use curves). This method is usually implemented with a java.awt.geom.FlatteningPathIterator, an implementation of PathIterator that approximates the curved segments in a given path with multiple line segments. The flatness argument to getPathIterator() is a measure of how closely these line segments must approximate the original curve segments, where smaller values of flatness imply a better approximation.

Copyright © 2001 O'Reilly & Associates. All rights reserved.