 | Chapter 7: Introduction to Cryptography |  |

In the next few chapters of this book, we're going to see how Java provides an interface to the algorithms required to perform the sort of authentications we've just talked about. We'll also explore the architecture Java provides for general implementation of these algorithms, including ones (such as encryption) that are not strictly required for authentication. If you're not familiar with the various cryptographic algorithms we've been alluding to so far in this chapter, the next section should sort that all out for you.
Essentially, all cryptographic operations are structured like the diagram in Figure 7-2. Central to this idea is the cryptographic algorithm itself, which is called an engine; the term "algorithm" is reserved to refer to particular implementations of the cryptographic operation. The engine takes some set of input data and (optionally) some sort of key and produces a set of output data. A few points are relevant to this diagram. There are engines that do not require a key as part of their input. In addition, not all cryptographic engines produce symmetric output--that is, it's not always the case that the original text can be reconstructed from the output data. Also, the size of the output is typically not the same as the size of the input. In the case of message digests and digital signatures, the output size is a small, fixed-size number of bytes; in the case of encryption engines, the output size is typically somewhat larger than the input size.
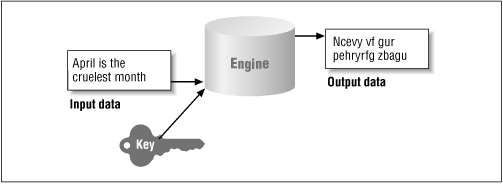
In the Java security package, there are two standard cryptographic engines: a message digest engine and a digital signature engine. In addition, for some users, an optional engine is available to perform encryption. Finally, because keys are central to the use of most of these engines, there is a wide set of classes that operate on keys, including engines that can be used to generate certain types of keys. The term "engine" is also used within the security package to refer to other classes that support these operations.
Message digests are the first cryptographic engines we'll examine. A message digest is the digital fingerprint we alluded to earlier. Conceptually, a message digest is a small sequence of bytes that is produced when a given set of data is passed through the message digest engine. Unlike other cryptographic engines, a message digest engine does not require a key to operate. It takes a single stream of data as its input and produces a single output. We call the output a message digest (or simply a digest, or a hash), and we say that the digest represents the input data.
The digest that corresponds to a particular set of data does not reflect any information about that data--in particular, there is no way to tell from a digest how much data it represents, or what the data actually was. A message digest is useful only when the data it represents is also available. If you want to determine whether a particular digest represents a particular set of data, you must recalculate the digest and compare the newly calculated digest with the original digest. If the two are equal, you've verified that the original digest does indeed represent the given set of data.
Data that is fed into a message digest engine is always treated as an ordered set of bytes. If even one byte of the data is altered or absent (or presented out of order), the digest will be different. Hence, a typical message digest algorithm has an internal accumulator that operates on all data fed into the engine. As each byte of data is fed into the engine, it is combined with the data in the accumulator to produce a new value, which is stored in the accumulator to provide input (see Figure 7-3).
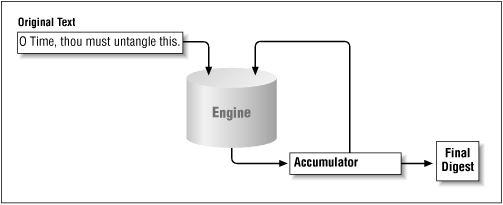
As a simple example, consider a message digest algorithm based on the exclusive-or of all the input bytes. The accumulator starts with a value of 0. If the string "O Time, thou must untangle this" is passed to the engine, the engine considers the bytes one at a time.[2] The first byte, "O", has a value of 0x4f, which will xor with the accumulator to provide a value of 0x4f. The next byte, a space (0x20), will xor with the accumulator to produce a value of 0x6f. And so on, such that the final result of the accumulator is 0x67.
[2]Don't be confused by the fact that we're dealing in bytes here, when the characters in a Java string are two bytes long. The data passed to the message digest engine is treated as arbitrary binary data--it doesn't matter if the data was originally ASCII (that is, byte-oriented) data, or a Java character string, or a binary class file.
There are a few differences between this example and a real message digest algorithm. First, standard algorithms typically operate on 4- or 8-byte quantities, so the bytes that are fed into the engine are first grouped into ints or longs, with padding added if the input data is not a multiple of the desired quantity. Second, they produce a digest that is usually 64 or 128 bits long, rather than a single byte; this final digest may be the value left in the accumulator, or it may be the value left in the accumulator subjected to additional operations.
The difference in the output size is one of the crucial differences. At best, the example we just walked through could produce 256 different digests. Any two given inputs have a 1 in 256 chance of producing the same digest, which is clearly not a sufficient guarantee that a digest represents a given set of data. In the example above, the string "O Time, thou must untangle this" produced a digest of 0x67--but so does the string "g". An algorithm that produces a 64-bit digest, on the other hand, produces over 18 quintillion unique digests, so that the odds that two data sequences will produce the same digest are very remote indeed.
This brings us to another of the crucial differences--a successful message digest algorithm must provide an assurance that it is computationally infeasible to find two messages that produce the same digest. This ensures that a new set of data cannot be substituted for the original data so that each produces the same digest.
Note also that a message digest in itself is not a secure entity. A digest is often provided with the data it represents; the recipient of the data then recalculates the digest to make sure that the data was not originally tampered with. But nothing in this scenario prevents someone from modifying both the original data and the digest, since both are transmitted, and since the calculation of the digest is a well-known operation requiring no key. Digests are an important piece of a digital signature, as we'll see in just a bit.
The second engine we'll look at generates cryptographic keys. Keys are the basis for many cryptographic operations. In its simplest sense, a key is a long string of numbers--not just any string of numbers, but a string of numbers that has very strict mathematical properties. The mathematical properties a key must have vary based on the cryptographic algorithms it is going to be used for, but there's an abstract (logical) set of properties all keys must have. It's this abstract set of properties that we'll see in the Java security package.
In the realm of cryptography, keys can either come alone (in which case they are called secret keys) or in pairs. A key pair has two keys, a public key and a private key. So altogether there are three types of keys--secret, public, and private--but from an algorithmic perspective, there are two types of keys, shared and secret.
When an algorithm requires a secret key, both parties using the algorithm will use the same key. Both parties must agree to keep the key secret, lest the security of the cryptography between the parties be compromised.
The secret key approach suffers from two problems. First, it requires a separate key for every pair of parties that need to send encrypted data. If you want to send your encrypted credit card data to ten different Internet stores, you would need ten different keys. Worse yet, if you operated an Internet store and had millions of customers, you would need literally millions of keys--one per customer. Management of such keys is a very hard problem.
The other problem with this approach is coming up with a method for sharing the keys. It's crucial that the key be kept secret, since anyone with the key can decrypt the data to be shared. Hence, you can't simply send the key over the network without somehow encrypting the key itself; doing so would be tantamount to sending the data itself unencrypted.
For these reasons, most keys in the security package are parts of public key/private key pairs (the exception to this is the encryption engine, which can use any type of key, and which provides a mechanism to share secret keys). Public and private keys can provide asymmetric operation to cryptographic engines. The public key can be used by one party participating in the algorithm, and the private key can be used by the other party.
The usefulness of this type of key pair is that one key can be published to the world. You can email your public key to your friends (and your enemies), you can put it on a global key server somewhere, you can broadcast it on the Internet--as long as you don't lose your private key, you can do anything you like with your public key.
Then, when someone wants to send you some sensitive information, they can use your public key to encrypt the data--and as long as you have kept your private key private, you'll be the only one who is actually able to decrypt the data. Similarly, when you want to send sensitive data to someone, all you need is their public key; when the data has been encrypted with the public key, you know that only the holder of the private key will be able to read what you've sent them. In the area of digital signatures, this key ordering is reversed: you sign a document with your private key, and the recipient of the document needs your public key in order to verify the digital signature.
Public key encryption is not without its key management problems as well, however. When you receive a digitally signed document, you need the public key of the signer of the document. The mechanism to obtain that key is very fluid; there are a number of proposals for centralized key warehouses that would hold public keys and for methods to access those keys, but the infrastructure to make this all a reality is not really in place. Hence, users of public keys have adopted a variety of techniques for obtaining the public keys.
The primary engine in the security package (at least as far as authentication goes) is the digital signature engine. Like a real signature, a digital signature is presumed to identify uniquely an entity (that is, an individual or an organization). Like a real signature, a digital signature can be forged, although it's much harder to forge a digital signature than a real signature.[3]Forging a digital signature requires access to the private key of the entity whose signature is being forged; this is yet another reason why it is important to keep your private keys private. Like a real signature, a digital signature can be "smudged" so that it is no longer recognizable. And because they're based on key certificates, digital signatures have other properties, such as the fact that they can expire.
[3]On the other hand, a forged digital signature is undetectable, unlike a forged real signature.
Digital signatures rely on two things: the ability to generate a message digest, and the ability to encrypt that digest. The entire process is shown in Figure 7-4.
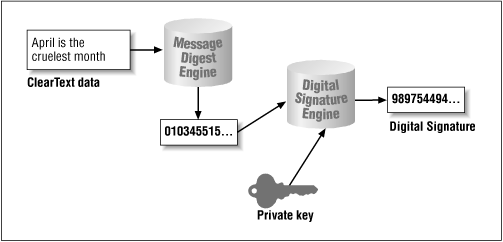
The process is as follows:
A message digest is calculated that represents the input data.
The digest is then encrypted with the private key.
Note that encryption is performed on the digest and not on the data itself. In order to present this signature to another entity, you must present the original data with it--the signature is just a message digest, and, as we mentioned earlier, you cannot reconstruct the input data from the message digest.
Verifying a digital signature requires the same path; the message digest of the original data must be calculated. This digest is then passed through the encryption engine, but this time, the public key of the signer is used. If the digital signature produced by this operation is the same as the digital signature that was presented, the digital signature is deemed valid. Alternately, for some digital signature algorithms, the signed digest could be decrypted with the public key, and the digests compared.
Nothing prevents the signed data from being intercepted. So the data that accompanies the digital signature cannot be sensitive data; the digital signature only verifies that the message came from a particular entity, but it does not actually protect that message.
However, just because someone can snoop the signed data does not mean that it can be tampered with--if the data is altered, it will not produce the same message digest, which in turn will not produce the same digital signature. And it's impossible to change the data, generate a new digest of that data, and then regenerate the digital signature without access to the private key. It is, however, possible to replace one message that was signed by a private key with another message that was signed by that same private key.
The final engine we'll discuss handles actual encryption. This engine is part of the Java Cryptography Extension (JCE) rather than the security package itself, and there are various rules on who may and may not obtain the JCE (at least from Sun or other U.S. companies). Encryption engines handle the encryption and decryption of arbitrary data, just as we would expect. An important thing to note is that the encryption engines that are part of the JCE are not used in the generation and verification of digital signatures--digital signatures use their own algorithms to encrypt and decrypt the message digest that are suitable only for manipulating data the size of a message digest. This difference allows the digital signature engine to be exportable, where the encryption engines are not.

Copyright © 2001 O'Reilly & Associates. All rights reserved.